지난 시간...
지난 시간에는 k-최근접 이웃 알고리즘을 사용하여 k-최근접 이웃 회귀 모델을 구현해보았다.
그 과정에서 결정계수의 점수에 따라서 모델이 과대적합인지 과소적합인지를 판단하는 방법과 해결 방안을 알아보았다.
오늘은 데이터 범위 밖에 있는 데이터를 예측해보는 모델을 만들어보는 시간을 가져보자.
지난시간에 했던 최근접 이웃 개수가 3인 모델을 가지고 진행을 해볼 것이다.
이 모델을 사용해 길이가 50cm인 농어의 무게를 예측해보자.
## 길이가 50cm인 농어의 무게 예측
print(knr.predict([[50]]))
## 출력값
[1033.33333333]모델에서는 길이가 50cm인 농어의 무게를 약 1,033g으로 예측했다. 하지만 실제로는 훨씬 더 많이 나간다고 한다.
문제점을 찾아보자
k-최근접 이웃 모델의 kneighbors() 메소드를 사용해 가장 가까운 이웃까지의 거리와 인덱스를 구하고, 길이가 50cm인 농어는 삼각형으로, 그 주변의 샘플은 마름모로 표시하여 산점도를 그려보자.
import matplotlib.pyplot as plt
## 50cm 농어의 이웃을 구한다.
distances, indexes = knr.kneighbors([[50]])
## 훈련 세트의 산점도를 그린다.
plt.scatter(train_input, train_target)
## 훈련 세트 중에서 이웃 샘플만 마름모 마커를 하여 표시
plt.scatter(train_input[indexes], train_target[indexes], marker = 'D')
## 50cm 농어 데이터 삼각형 마커로 표시
plt.scatter(50, 1033, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()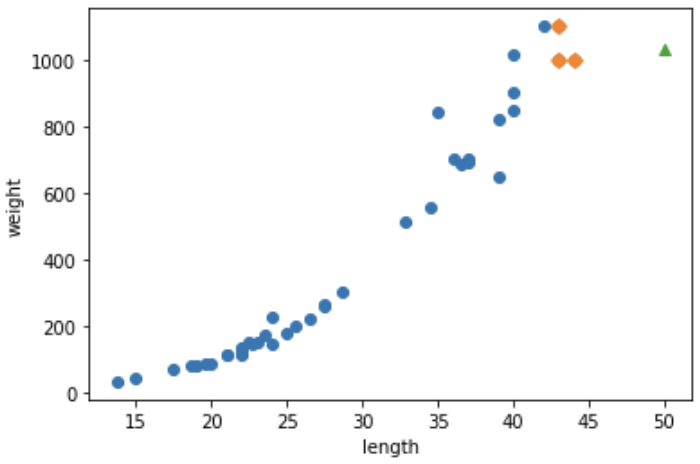
선형 회귀
선형회귀는 어떤 직선을 학습하는 알고리즘이다. 비교적 간단하고 성능이 뛰어나 맨 처음 배우는 머신러닝 알고리즘이며 널리 사용되는 회귀 알고리즘이다.
지난 시간에 농어의 길이에 대한 농어의 무게 산점도를 보면 데이터가 우상향으로 증가하는 것을 알 수 있다. 따라서 우상향 직선이 농어 데이터를 잘 나타낼 수 있을 것이다.
사이킷런은 sklearn.linear_model 패키지 아래에 LinearRegression 클래스로 선형 회귀 알고리즘을 구현해 놓았다. 이 클래스에서도 fit(), score(), predict() 메소드를 가지고 훈련, 성능 측정, 예측한다.
이제 선형 회귀 모델을 만들어보자
## 사이킷런은 sklearn.linear_model 패키지 아래에 LinearRegression에 선형 알고리즘이 구현되어 있다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
## 선형 회귀 모델을 훈련한다.
lr.fit(train_input, train_target)
## 50cm 농어에 대해 예측한다.
print(lr.predict([[50]]))
## 출력값
[1241.83860323]k-최근접 이웃 회귀를 사용했을 때와 달리 선형 회귀의 경우 농어의 무게를 더 높게 예측했다 이러한 이유를 아래에서 알아보자.
직선의 방정식은 $y=a \times x + b$이다. 이를 y를 농어 무게, x를 농어 길이로 변환하면 $농어 무게 = a \times 농어 길이 + b$이다.
LinearRegression 클래스는 위 방정식의 a, b의 최적값을 알아서 찾아내어 lr객체의 coef_와 intercept_ 속성에 저장한다.
print(lr.coef_, lr.intercept_)
## 출력값
[39.01714496] -709.0186449535477LinearRegression 클래스가 찾은 최적의 직선의 방정식과 훈련 세트의 산점도를 그래프로 표현해보자.
## 훈련 세트의 산점도를 그린다.
plt.scatter(train_input, train_target)
## 길이 15~50cm의 농어 직선
plt.plot([15, 50], [15*lr.coef_ + lr.intercept_, 50*lr.coef_ + lr.intercept_])
## 50cm 농어 데이터
plt.scatter(50, 1241.8, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

길이가 50cm인 농어는 직선 위에 존재한다. 선형 회귀를 통해 훈련 세트 범위를 벗어난 농어의 무게도 예측할 수 있게 되었으므로 훈련 세트와 테스트 세트에 대한 결정계수 점수를 확인해보자.
## 훈련 세트와 테스트 세트에 대한 R^2 점수를 확인
print(lr.score(train_input, train_target))
print(lr.score(test_input, test_target))
## 출력값
0.939846333997604
0.8247503123313558테스트 세트의 점수가 훈련 세트의 점수에 비해 너무 낮지만 훈련 세트의 점수도 높지 않은 편이라 과소적합되었다고 봐야한다.
다항 회귀
선형 회귀는 직선이 왼쪽 아래로도 무한이 뻗어있다. 농어의 무게는 0g 이상이기 때문에 이는 현실에서는 있을 수 없는 일이다.
사실 농어의 길이와 무게에 대한 산점도를 보면 일직선보다 살짝 구부러진 곡선에 가깝다.
최적의 곡선을 찾기 위해서는 2차 방정식을 그려야하므로 길이를 제곱한 항이 훈련 세트에 추가되어야 한다.
column_stack() 함수를 사용하여 제곱항을 추가한다.
## 길이 제곱을 추가
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))
## 훈련 세트, 테스트 세트 크기 확인
print(train_poly.shape, test_poly.shape)
## 출력값
(42, 2) (14, 2)2차항을 추가한 데이터를 가지고 선형 회귀 모델을 다시 훈련해보자. 훈련 세트에 2차항을 추가했지만 타깃값은 그대로 사용해야한다.
타깃값은 어떤 그래프를 훈련하든지 바꿀 필요가 없다.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]]))
## 출력값
[1573.98423528]
## 훈련한 계수와 절편을 출력
print(lr.coef_, lr.intercept_)
## 출력값
[ 1.01433211 -21.55792498] 116.05021078278272차항을 넣기 전 모델보다 더 높은 값을 예측했다. 이 모델은 아래와 같은 그래프를 학습했다.
$$무게 = 1.01 \times 길이^2 - 21.6 \times 길이 + 116.05 $$
위처럼 다항식을 사용한 선형 회귀를 다항 회귀라고 부른다. 이제 훈련 세트의 산점도에 그래프로 다항식을 그려보자. 짧은 직선을 이어서 그리면 곡선을 표현할 수 있다.
## 구간별 직선을 그리기 위해 15에서 49까지 정수 배열을 만든다.
point = np.arange(15, 50)
## 훈련 세트의 산점도를 그린다.
plt.scatter(train_input, train_target)
## 15에서 49까지 2차 방정식 그래프를 그린다.
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
## 50cm 농어 데이터
plt.scatter(50, 1574, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
훈련 세트의 경향을 잘 따르고 있고, 그래프가 음수로 나오는 일도 없기 때문에 단순 선형 회귀 모델보다 더 나은 그래프가 그려졌다.
이제 훈련 세트와 테스트 세트의 $R^2$점수를 평가해보자.
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
## 출력값
0.9706807451768623
0.9775935108325122훈련 세트와 테스트 세트에 대한 점수가 크게 높아졌지만 테스트 세트 점수가 훈련 세트 점수보다 조금 더 높기 때문에 과소적합이 아직 남아있다고 볼 수 있다.
다음 시간에는 더 복잡한 모델로 과소적합을 해결해보자.
정리
1. 선형 회귀: 특성과 타깃 사이의 관계를 잘 나타내는 선형 방정식을 찾는다.
2. 선형 회귀가 찾은 특성과 타깃 사이의 관계는 선형 방정식의 계수 또는 가중치에 저장된다.
3. 다항 회귀: 다항식을 사용해 특성과 타깃 사이의 관계를 나타낸다. 비선형일 수 있지만 선형 회귀로 표현할 수 있다.
'혼자 공부하는 머신러닝 + 딥러닝' 카테고리의 다른 글
| 혼자 공부하는 머신러닝 + 딥러닝 Day 7 (0) | 2022.09.08 |
|---|---|
| 혼자 공부하는 머신러닝 + 딥러닝 Day 6 (0) | 2022.09.08 |
| 혼자 공부하는 머신러닝 + 딥러닝 Day 4 (0) | 2022.08.29 |
| 혼자 공부하는 머신러닝 + 딥러닝 Day 3 (0) | 2022.08.24 |
| 혼자 공부하는 머신러닝 + 딥러닝 Day 2 (0) | 2022.08.16 |