선택 정렬(Selection Sort)
리스트에서 아직 정렬 안된 부분의 원소들 중에서 최솟값을 '선택'하여 정렬 안된 부분의 가장 왼쪽의 원소와 교환하는 정렬 알고리즘.
동작 방법
숫자 20, 4, 2, 1, 50, 31, 13, 7 이 준비되어 있다. 정렬된 데이터는 색으로 표시한다.

1) 정렬되지 않은 원소 중 가장 작은 '1'을 선택해 정렬 안된 부분의 가장 왼쪽에 있는 '20'과 교환해준다.

교환된 '1'이 가장 왼쪽에 위치하고 '20'은 '1'의 자리에 들어있다.
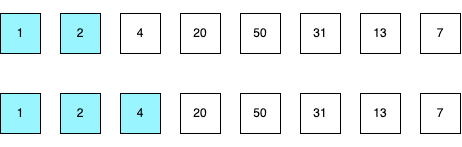
2) 정렬되지 않은 원소 중 가장 작은 '2'를 선택해 정렬 안된 부분의 가장 왼쪽에 있는 '4'와 교환해준다.

교환된 '2'가 '1' 다음에 정렬되고 '4'는 '2'의 자리에 들어있다.
3) '4'는 정렬되지 않은 수 중에서 가장 작은 수 이므로 그 자리에서 정렬한다.
4) 이를 반복하면 1, 2, 4, 7, 13, 20, 31, 50 순으로 정렬된다.

실습
위의 동작 방법이 옳은 지 실습을 통해 확인해보자.
숫자 20, 4, 2, 1, 50, 31, 13, 7 이 준비되어 있다.
## 데이터 준비
array = [20, 4, 2, 1, 50, 31, 13, 7]데이터를 리스트에 저장해 준비해준다.
for i in range(len(array)): ## 리스트의 크기만큼 for문을 돌려준다.
## 정렬되지 않은 원소 중 가장 앞에 위치한 원소의 인덱스
min_index = i
## 정렬되지 않은 원소 중 가장 작은 원소 찾기
for j in range(i+1, len(array)):
if array[min_index] > array[j]:
min_index = j
## 정렬되지 않은 원소 중 가장 작은 원소와 정렬되지 않은 원소 중 가장 왼쪽에 위치한 원소와 자리 교환
array[min_index], array[i] = array[i], array[min_index]선택 정렬을 수행한다.
print(array)
## 출력값
[1, 2, 4, 7, 13, 20, 31, 50]선택 정렬 후 리스트를 출력하면 오름차순으로 정렬되어 있는 것을 알 수 있다.
수행시간
선택 정렬은 1회 반복마다 정렬 안된 부분에서 가장 작은 원소를 선택한다. 따라서 N개의 원소가 있다고 가정했을 때 처음 반복을 실행하면 최솟값을 찾기 위해 N-1회, 2번 째 반복 시 N-2회의 원소 비교가 필요하다. 시간 복잡도를 식으로 표현하면 아래와 같다.
$$ (N-1) + (N-2) + \cdots + 2 + 1 = {N(N-1) \over 2} = O(N^2) $$
선택 정렬은 항상 $O(N^2)$의 시간 복잡도를 갖기 때문에 민감하지 않은 알고리즘이지만 효율성이 떨어져 거의 활용하지 않는다.
정리
1. 선택 정렬은 정렬 되지 않은 원소 중 최솟값을 '선택'해 정렬 안된 원소와 위치를 바꾼다.
2. 시간 복잡도는 $O(N^2)$이다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 계수 정렬 (0) | 2022.11.04 |
|---|---|
| [알고리즘]삽입 정렬 (0) | 2022.09.15 |
| [자료구조]큐 (0) | 2022.09.13 |
| [자료구조]스택 (0) | 2022.09.13 |
| [자료 구조] 이진트리(Binary Tree) (0) | 2022.08.25 |